射线法介绍

在地图应用上，我们会经常需要判断一个点是否位于多边形区域内，这里介绍下采用射线法如何实现。

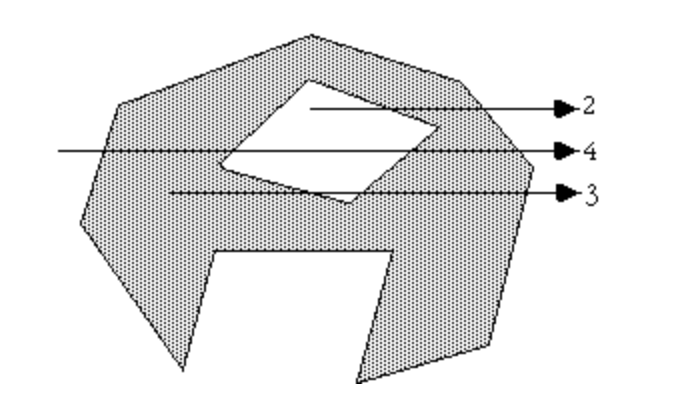
算法思想：从待判断的点向某一个方向引射线，计算和多边形交点的个数，如果个数是偶数或者0，则点在多边形外，如果是奇数，则在多边形内，如下图： 这里有两种情况需要特殊处理：

• 1） 射线经过顶点：当射线经过顶点时，判断就会出现异常情况。
• 2） 点在边上：这种情况也不能用交点个数的奇偶性来判断了，要快速地判断这个点是否在边上：

GeoUtils.isPointInPolygon = (point, polygon)=> {
 if(!point || point.length<2) {
  console.error('坐标点格式错误')
  return false;
 }
 if(!polygon || polygon.length<4) {
  console.error('多边形格式错误')
  return false;
 }

 var pts = JSON.parse(JSON.stringify(polygon));
 // 下述代码来源：http://paulbourke.net/geometry/insidepoly/，进行了部分修改
 // 基本思想是利用射线法，计算射线与多边形各边的交点，如果是偶数，则点在多边形外，否则
 // 在多边形内。还会考虑一些特殊情况，如点在多边形顶点上，点在多边形边上等特殊情况。

 var boundOrVertex = true; // 如果点位于多边形的顶点或边上，也算做点在多边形内，直接返回true
 var intersectCount = 0; // cross points count of x
 var precision = 2e-10; // 浮点类型计算时候与0比较时候的容差
 var p1, p2; // neighbour bound vertices
 var p = point; // 测试点
 var N = pts.length;

 p1 = pts[0]; //left vertex 左顶点
 for (var i = 1; i <= N; ++i) { // check all rays
  if (p.lat == p1.lat && p.lng ==p1.lng) { // 如果点位于多边形的顶点或边上，也算做点在多边形内，直接返回true
   return boundOrVertex; // p is an vertex
  }

  p2 = pts[i % N]; // right vertex 右顶点
  // 如果判断点小于（p1、p2纬度最小） 或者 判断点 大于（p1、p2纬度最大） 如果全部不符合大于最小，小于最大的条件intersectCount = 0 没有处于内部
  if (p.lat < Math.min(p1.lat, p2.lat) || p.lat > Math.max(p1.lat, p2.lat)) { // ray is outside of our interests
   p1 = p2;
   continue; // next ray left point
  }

  // 如果纬度 大于最小并且小于最大，说明处于中间
  if (p.lat > Math.min(p1.lat, p2.lat) && p.lat < Math.max(p1.lat, p2.lat)) { // ray is crossing over by the algorithm (common part of)
   if (p.lng <= Math.max(p1.lng, p2.lng)) { //x is before of ray 经度小于p1、p2最大
    // 如果纬度p1、p2相等。并且 判断点 大于等于 最小的经度 （也就是说他们处于一条水平上）
    if (p1.lat == p2.lat && p.lng >= Math.min(p1.lng, p2.lng)) { // overlies on a horizontal ray
     return boundOrVertex;   
    }

    if (p1.lng == p2.lng) { // ray is vertical
     if (p1.lng == p.lng) { // overlies on a vertical ray 
      return boundOrVertex;
     } else { // before ray
      ++intersectCount;
     }
    } else { // cross point on the left side
     // 直线的斜率k=(y2-y1)/(x2-x1) 故直线方程为y-y1=(y2-y1)/(x2-x1)×(x-x1)
     var xinters = (p.lat - p1.lat) * (p2.lng - p1.lng) / (p2.lat - p1.lat) + p1.lng; // cross point of lng
     if (Math.abs(p.lng - xinters) < precision) { // overlies on a ray
      return boundOrVertex;
     }

     if (p.lng < xinters) { // before ray
      ++intersectCount;
     }
    }
   }
  } else { // special case when ray is crossing through the vertex
   if (p.lat == p2.lat && p.lng <= p2.lng) { //p crossing over p2
    var p3 = pts[(i + 1) % N]; //next vertex
    if (p.lat >= Math.min(p1.lat, p3.lat) && p.lat <= Math.max(p1.lat, p3.lat)) { //p.lat lies between p1.lat & p3.lat
     ++intersectCount; 
    } else {
     intersectCount += 2; 
    }
   }
  }
  p1 = p2; //next ray left point
 }

 if (intersectCount % 2 == 0) { // 偶数在多边形外
  return false;
 } else { // 奇数在多边形内
  return true;
 }
}

参考文献 (opens new window)