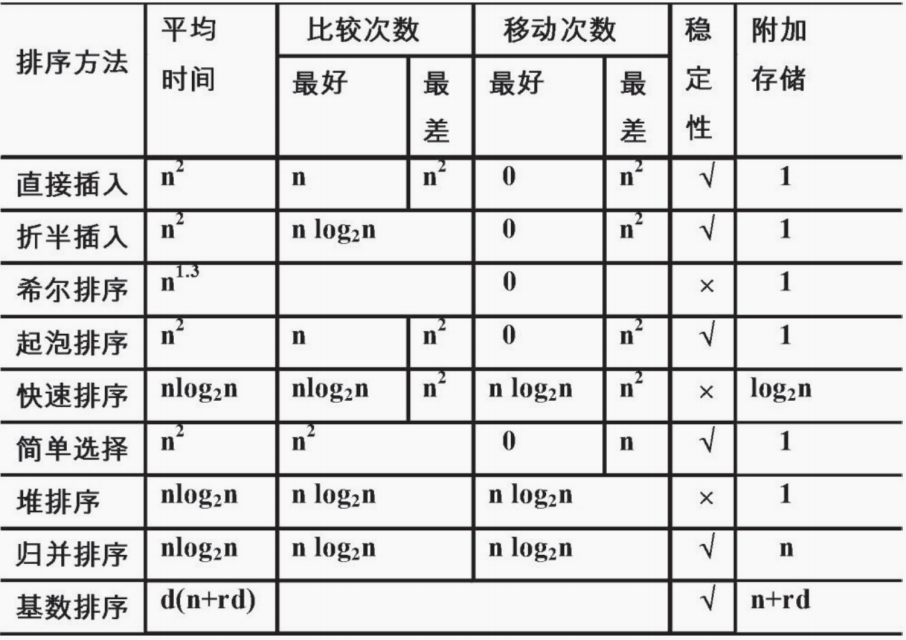
排序算法分类

规则不同可以分为：插入排序、交换排序、选择排序、归并排序、基数排序
时间复杂度不同：简单排序O（n^2）、先进排序O(nlog2^n)

插入排序

基本思想：
每一步将一个待排序的对象，按其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止。
即边插入边排序，保证子序列中随时都是排好序的
具体实现的3️⃣种不同算法：
直接插入排序（基于顺序查找） | 最简单的排序法
折半插入排序（基于折半查找）
希尔排序（基于逐趟缩小增量）

1️⃣直接插入排序

排序过程：整个排序过程为n-1趟插入，即先将序列中第1个记录看成是一个有序序列，然后从第2个记录开始，逐个进行插入，直至整个序列有序。

// javascript
let temp;
function InsertSort(L){
  let i,j;
  for(i = 1; i < L.length; i++){
    if(L[i] < L[i-1]){
      temp = L[i];
      L[i] = L[i-1];
      for(j = i-1; temp < L[j]; --j){
        L[j+1]=L[j]
      }
      L[j+1] = temp;
    }
  }
  return L;
}
console.log(InsertSort([2,6,3,1,4]))

时间复杂度：O（n^2）
空间复杂度：O（1）
是一种稳定的排序方法

2️⃣折半插入排序

在插入r[i]时，利用折半查找法寻找r[i]的插入位置

// javascript
let temp;
function BInsertSort(L){
  for(i = 1; i < L.length; ++i){
    temp = L[i];
    low = 0;
    high= i - 1;
    while(low <= high){ // 小 到 大
      m = Math.floor((low + high) / 2);
      if(temp < L[m]) {
        high = m - 1;
      } else {
        low = m + 1;
      }
    }
    for( j = i; j > high + 1; --j){
      L[j] = L[j-1];
    }
    L[high+1] = temp;
  }
  return L;
}
console.log(BInsertSort([8,2,3,1,5,6,4]));

折半插入排序算法分析
减少了比较次数，但没有减少移动次数
平均性能优于直接插入排序
时间复杂度为O（n^2)
空间复杂度为O(1)
是一种稳定的排序方法

3️⃣希尔排序

算法思想的出发点：
直接插入排序在基本有序时，效率较高
在待排序的记录个数较少时，效率较高
基本思想：
先将整个待排序记录序列分割成若干子序列，分别进行直接插入排序，待整个序列中的记录”基本有序“时，再对全体记录进行一次直接插入排序
希尔排序技巧：
子序列的构成不是简单地”逐段分割“
将相隔某个增量dk的记录组成一个子序列
让增量dk逐趟缩短（例如依次取5，3，1）
直到dk=1为止
😄优点：
小元素跳跃式前移
最后一趟增量为1时，序列已基本有序
平均性能优于直接插入排序

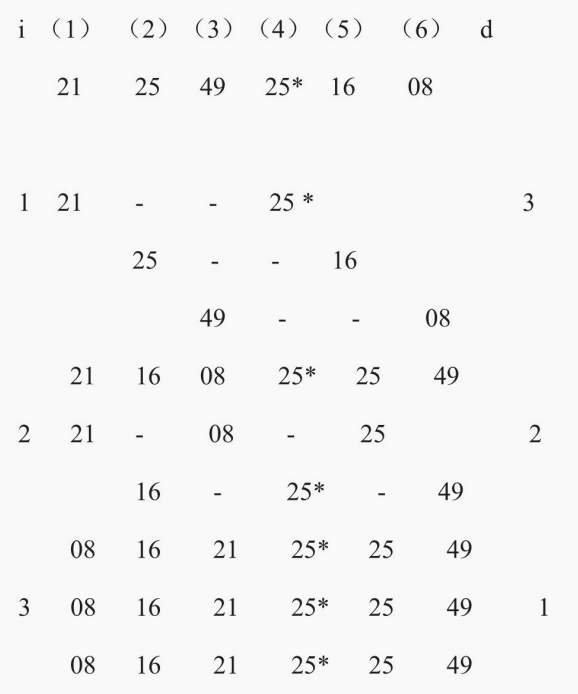
希尔排序算法主程序

// javascript
/**
 * L 数组
 * dlta 增量
 * */
function ShellSort( L, dlta){ // dk的值依次装在dlta中
  // 按增量序列dlta[0...t-1]对顺序表L作shell排序
  for ( k = 0; k < dlta.length; ++k) {
    ShellInsert( L, dlta[k]); // 增量为dlta[k]的一趟排序
  }
  return L;
}

let temp;
function ShellInsert( L, dk){
  for ( i = dk; i < L.length; ++i){
    if (L[i] < L[i - dk]) {
      temp = L[i]; // 暂时存在r[0]
      for ( j = i - dk; j >= 0 && (temp < L[j]); j = j - dk) {
        L[j+dk] = L[j];
      }
      L[j + dk] = temp;
    }
  }
}
console.log(ShellSort([21,25,49,25,16,18,9,88,7,3,6,30],[3,1]))

算法分析： 时间复杂度是n和d的函数： O（n^1.25)~O(1.6n^1.25)--经验公式
空间复杂度O（1）
是一种不稳定的排序算法
如何选择d序列，目前尚未解决
最后一个增量值必须为1，无除1以后的公因子
不宜在链式存储结构中实现

交换排序

基本思想：
两两比较，如果发生逆序则交换，直到所有记录都排好序为止。

1️⃣起泡排序O(n^2)

// javascript冒泡
function bubble_sort(L){
  let m, i, j, flag = 1;
  m = L.length - 1;
  while (( m >= 0 ) && ( flag == 1 )) {
    flag = 0;
    for ( j = 0; j < m; j++) {
      if (L[j] > L[j + 1]) { // 从小到大排
        flag = 1;
        [L[j],L[j+1]] = [L[j+1],L[j]]; // 交换数据
      }
    }
    m--;
  }
  return L;
}
console.log(bubble_sort([21,25,49,25,16,18,9,88,7,3,6,30]));

算法分析：
设对象个数为n
比较次数和移动次数与初始排列有关
最好的情况下：
只需1趟排序，比较次数为n-1，不移动 最坏的情况下：
时间复杂度为O（n^2)
空间复杂度为O（1） 是一种稳定的排序方法

2️⃣快速排序O(nlog2^n)

基本思想：
取一个元素（如第一个）为中心
所有比它小的一律放前，比它大的一律放后，形成的左右两个子表；
对各子表重新选择中心元素并依此规则调整，直到每一个子表的元素只剩一个
快速排序的特点：

1. 每一趟的子表的形成采用从两头向中间交替式逼近法
2. 由于每趟中对各子表的操作都相似，可以采用递归算法

// 快排
function Qsort( L, low, high){
  if(low <= high){
    pivotloc = Partition(L, low, high);
    Qsort(L, low, pivotloc - 1);
    Qsort(L, pivotloc + 1, high);
  }
  return L;
}
// 快速排序的一次划分
function Partition( L, low, high) {
  let temp = L[low];
  pivotkey = L[low];
  while (low < high) {
    while (low < high && L[high] >= pivotkey) {
      --high;
    }
    [L[low],L[high]] = [L[high], L[low]]; // 交换两个位置
    while (low < high && L[low] <= pivotkey) {
      ++low;
    }
    [L[low],L[high]] = [L[high], L[low]]; // 交换位置
  }
  return low;
}
let L = [21,25,49,25,16,18,9,88,7,3,6,30]
console.log(Qsort(L, 0, L.length-1));

算法分析：
平均计算时间是O（nlog2n）
实验结果表明：就平均计算时间而言，是我们所讨论的所有内部排序方法中最好的一个。
快速排序是递归的，需要有一个栈存放每次递归调用时的参数（新的low和high）
最大递归调用层次数与递归树的深度一致。因此要求存储开销O(nlog2n)
最好：划分后，左右侧子序列长度相同
最坏：从小到大排序，递归树成为单支树，每次划分只得到一个比上一次少一个对象的子序列，必须经过n-1趟才能把所有的对象定位，而且第i趟需要经过n-1次关键码比较，才能找到第i个对象的安放位置
快速排序算法分析：
时间效率：O（nlog2n） 每一趟确定的元素程指数增加
空间效率：O（nlog2n） 递归要用到的栈空间
稳定性：不稳定 可选任意元素为支点

选择排序

基本思想：
每一趟在后面n-i+1中，选中关键码最小的对象，作为有序序列的第i个记录，简单选择排序示例

简单选择排序：

// javascript选择排序
function selectSort( L ){
  for (i = 0; i < L.length; i++) {
    k = i;
    for (j = i + 1; j < L.length; j++) {
      if ( L[j] < L[k] ) {
        k = j;
      }
    }
    if (k != i) {
        [L[i],L[k]] = [L[k],L[i]]
    }
  }
  return L
}
let L = [21,25,49,25,16,18,9,88,7,3,6,30]
console.log(selectSort(L));

算法分析
移动次数
最好的情况0
最坏情况：3(n-1)
时间复杂度：O(n^2)
空间复杂度：O(1) 稳定性：稳定

堆排序

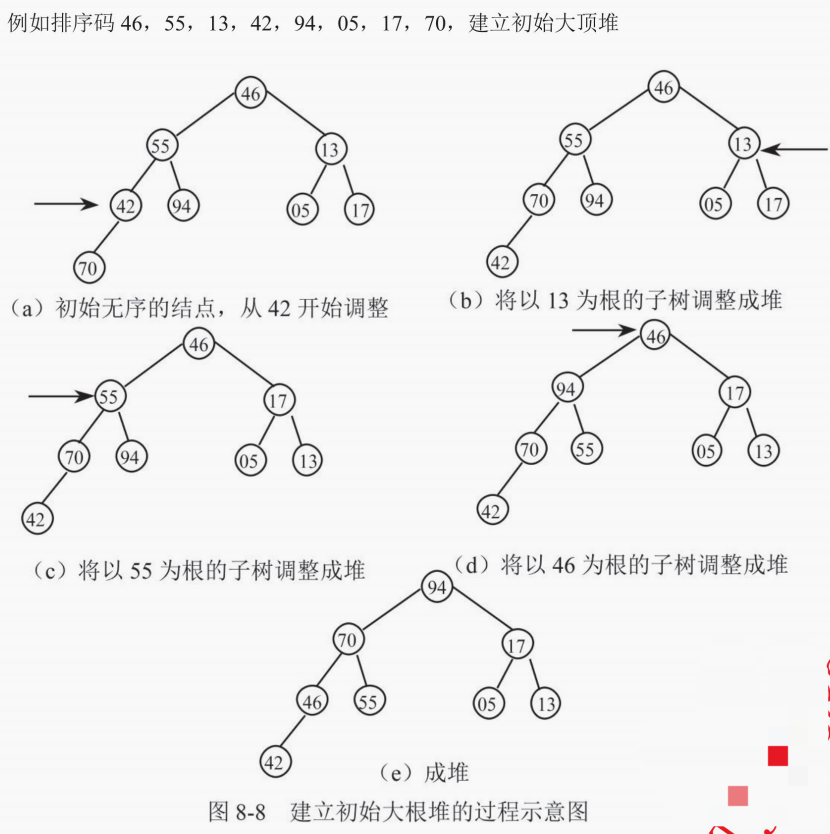
如果将序列看成一个完全二叉树，非终端结点的值均小于或大于左右子结点的值。
大顶堆的排序思想： 大顶堆顶点是最大的值，把顶点拿出来和完全二叉树最后一个结点进行交换，把除掉这个节点之外的节点重新调整成大顶堆。
如何在输出堆顶元素后调整，使之成为新堆？

1. 输出堆顶元素后，以堆中最后一个元素替代之
2. 大顶堆排序时将根结点与左、右子树根结点比较，并与最大者交换
3. 重复直至叶子节点，得到新的堆

// javascript
// 大顶堆
function adjustHeap( L, i, length){
    for (k = i * 2 + 1; k < length; k = k + 2) {// 从i结点的左子结点开始，也就是2i+1处开始
        if ( k + 1 < length && L[k] < L[k+1]) {// 先找出两个子节点中最大的
            k++;
        }
        if (L[k] > L[i]) {// 如果子节点大于父节点，将子节点值赋给父节点
            [L[i],L[k]] = [L[k],L[i]]; // 交换
        } else {
            break;
        }
    }
}

function sort( arr ) {
    // 1.构建大顶堆
    for(i = arr.length / 2 - 1; i >= 0; i--){
        // 从第一个非叶子结点从下至上，从右至左调整结构
        adjustHeap( arr, Math.floor(i), arr.length);
    }
    // 2.调整堆结构+交换堆顶元素与末尾元素
    for( j = arr.length - 1; j > 0; j--){
        [arr[0],arr[j]] = [arr[j], arr[0]];// 将堆顶元素与末尾元素进行交换
        adjustHeap(arr,0,j);// 重新对堆进行调整
    }
    return arr;
}

let arr = [9,8,7,6,5,4,3,2,1];
// let arr = [21,25,49,25,16,18,9,88,7,3,6,30];
console.log(sort(arr));

归并排序 （二路归并）

归并：将两个或两个以上的有序表组合成一个新的有序表
2路归并排序过程：
初始序列看成n个有序子序列，每个子序列长度为1
两两合并，得到[n/2]个长度为2或1的有序子序列
再两两合并，重复直至得到一个长度为n的有序序列为止
时间复杂度：O（nlog2n)
空间效率：O(n)
稳定性：稳定

// 归并排序
function　merge(left, right){
    var　result=[];
    while (left.length > 0 && right.length > 0){
        if (left[0] < right[0]) {
            /*shift()方法用于把数组的第一个元素从其中删除，并返回第一个元素的值。*/
            result.push( left.shift() );
        } else {
            result.push(right.shift());
        }
    }
    return　result.concat(left).concat(right);
}
function　mergeSort(items){
    if(items.length == 1){
        return　items;
    }
    var　middle = Math.floor(items.length/2),
    left = items.slice(0, middle),
    right = items.slice(middle);
    return　merge(mergeSort(left), mergeSort(right));
}
let L = [21,25,49,25,16,18,9,88,7,3,6,30];
console.log(mergeSort(L));

基数排序

前面的排序方法主要通过关键字值之间的比较和移动，基数排序不需要关键字之间的比较
关键字排序：

1. 最高位优先MSD（Most Significant Digit first）
2. 最低位优先LSD（Least Significant Digit first)
3. 链式基数排序：用链表作存储结构的基数排序

// 基数排序
function maxbit( data, n) //辅助函数，求数据的最大位数
{
    let d = 1; //保存最大的位数
    let p = 10;
    for( i = 0; i < n; ++i)
    {
        while(data[i] >= p)
        {
            p *= 10;
            ++d;
        }
    }
    return d;
}
function radixsort( data, n) //基数排序
{
    let d = maxbit(data, n);
    let tmp = [];
    let count = []; //计数器
    let i, j, k;
    let radix = 1;
    for (i = 0; i < d; i++) {//进行d次排序
        for (j = 0; j < 10; j++) { // 初始化数组
            tmp[j] = []; 
        }

        for (j = 0; j < data.length; j++) {
            k = Math.floor((data[j] / radix)) % 10; 
            let td = data[j];
            tmp[k].push(td); // 装桶

        }
        data = [];
        for(j = 0; j < n; j++){ // 将临时数组的内容复制到data中
            for( k = 0; k < tmp[j].length; k++) {
                data.push(tmp[j][k]);
            }
        } 
        radix = radix * 10;
    }
    return data;
}
let L = [21,25,49,25,16,18,9,88,7,3,6,30];
console.log(radixsort(L, 10));

方法1️⃣:最高位优先法

先对最高位关键字k1（如花色）排序，将序列分成若干子序列，每个子序列有相同的值：
然后让每个子序列对次关键字k2（如面值）排序，又分成若干更小的子序列：
最高位优先法
依次重复，直至就每个子序列对最低位关键字kd排序，就可以得到一个有序的序列
十进制数比较可以看作是一个多关键字排序
最高从头再来优先法，如果位数不足可以往前补0
用MSD关键字序列排序
{278,109,063,064,930,589,184,505,269,008,083}
按最高位排序
{063，064，008，083}，{109，184}，{278，269}，{589，505}，{930}
最次高位排序
{008},{063,064},{083},{109},{184},{269},{278},{505},{589},{903}
按最低位排序
{008},{063},{064},{083},{109},{184},{269},{278},{505},{589},{903}
最后将所有的子序列依次链接在一起就得到排好的序列

方法2️⃣:最低位优先法

首先依据最低位排序码Kd对所有对象进行一趟排序再依据次低位排序码Kd-1对上一次排序结果排序依次重复，直到依据排序码K1最后一趟排序完成，就可以得到一个有序序列。
这种方法不需 要再分组，而是整个对象组都参加排序
最低位优先法
278，109，063，930，184，589，269，008，083
按个位排序
930，063，083，184，278，008，109，589，269
按十位排序
008，109，930，063，169，278，083，184，589 按百位排序
008，063，083，109，169，184，278，589，930

方法3️⃣:链式基数排序

先决条件：
-- 知道各级关键字的主次关系 -- 知道各级关键字的取值范围
利用”分配“和”收集”对关键字进行排序：
首先对低位关键字排序，各个记录按照此位关键字的值“分配”到相应的序列里。
按照序列对应的值的大小，从各个序列中将记录“收集”，收集后的序列按照些位关键字有序。
算法分析
n个记录，每个记录有d位关键字，关键字取值范围rd（如十进制为10）。重复执行d趟“分配”与”收集“，每趟对n个记录进行“分配”，对rd个队列进行“收集”
需要增加n+2rd个附加链接指针
链式基数排序算法分析：
时间效率：O（d（n+d）） 空间效率：O（n+rd）
稳定性：稳定
排序算法比较