Glittering's blog
mamingjuan
2020-10-10
目录

图的定义及应用

# 图的定义

图是由顶点集 V 和顶点间的关系集合 E（边的集合）组成的一种数据结构，可以用二元组定义为：G=（V，E）

# 基本术语

  1. 有向图和无向图
    在图中，若用剪头标明了边是有方向性的，称这样的图为有向图，否则称无向图
  2. 完全图、稠密图、稀疏图
    具有 n 个顶点，n(n-1)/2 条边的图，称为完全无向图
    具有 n 个顶点，n(n-1)条弧的有向图，称为完全有向图。
    完全无向图和完全有向图都称为完全图。
    对于一般无向图，顶点数为 n，边数为 e，则 0<=e<=n(n-1)/2
    对于一般有向图，项点数为 n，弧数为 e，则 0<=e<=n(n-1)
    当一个图接近完全图时，则称它为稠密图，相反，当一个图含有较少的边或者弧则称为稀疏图
  3. 度、入度、出度
    在图中，一个顶点依附的边或弧的数目，称为该顶点的度。
    在有向图中，一个顶点依附的弧头数目，称为顶点的入度，一个顶点依附的弧尾数目，称为该顶点的出度，某个顶点的入度和出度这和称为该顶点的度。

# 图的存储

图的存储结构可以分为5种：

  1. 邻接矩阵 图的邻接矩阵存储方式是用两个数组来表示图：
    一个一维数组存储图中顶点信息；（顶点数组）
    一个二维数组（称为邻接矩阵）存储图中边或弧的信息（边数组）
  2. 邻接表
    邻接矩阵是一种不错的图存储结构。 但是：对于边树相对顶点较少的图，这种结构是存在存储空间的极大浪费的。
    因此我们考虑先进一步，使用邻接表存储.
  3. 十字链表 对于有向图而言，邻接表也是有缺陷的。 试想想哈，关心了出度问题，想了解入度问题就必须把整个图遍历才能知道。 反之，逆邻接表解决了入度问题却不了解出度的情况。 那是否可以将邻接表和逆邻接表结合起来呢？答案是肯定的。 这就是所谓的存储结构：十字链表。
  4. 邻接多重表 有向图的优化存储结构为十字链表。
    对于无向图的邻接表，有没有问题呢？如果我们要删除无向图中的某一条边时？
    那也就意味着必须找到这条边的两个边节点并进行操作。其实还是比较麻烦的。于是出现的邻接多重表
  5. 边集数组 边集数组侧重于对边依次进行处理的操作，而不适合对顶点相关的操作。
    边数集由两个一维数组组成，一个存储顶点信息，一个存储边的信息，包括起点下标（start），终点下标（end）和权值（weight）

# 图的遍历

两条遍历图的算法：

  1. 深度优先遍历（Depth_First_Search）,也称为深度优先搜索，简称DFS
  2. 广度优先遍历（Breadth_First_Search）,又称为广度优先搜索，简称BFS。

深度遍历类似树的前序遍历，广度优先遍历类似于树的层序遍历。

# 深度优先搜索

深度优先搜索采用的思想🔖:类似于树的先序遍历（根左右）

  1. 首先访问顶点 i，并将其访问标记置为访问过，即 visited[i]=1;
  2. 然后搜索与顶点 i 有边相连的下一个顶点 j，若 j 未被访问过则访问它，并将 j 的访问标记置为已访问过，visited[j]=1,然后从 j 开始重复此过程，若 j 已访问，再看与 i 有边连的其它顶点；
  3. 若与 i 有边相连的顶点都被访问过，则退回到前一个访问顶点并重复刚才过程，直到图中所有顶点都被访问过为止。

# 广度优先搜索

广度优先搜索采用的思想🔖：队列

  1. 开始时要将其置空
  2. 在每访问一个顶点时，要将其入队
  3. 在访问一个顶点的所有后继时，要将其出队。
  4. 若队列为空时，说明每个访问过的顶点的所有后继均已访问完毕，因而本次遍历可以结束。若此时还有未访问的顶点，需要另选起点进行遍历。

# 图的应用（四大应用）

# 关于图的几个概念定义：

  1. 连通图：在无向图中，若任意两个顶点 i 到顶点 j 有路径相连（当然从 j 到 i 也一定有路径）。则称该无向图为连通图。
  2. 强连通图：在有向图中，若任意两个顶点 i 到 j 有路径相连，则称该有向图为强连通图。
  3. 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
  4. 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部 n 个顶点，但只有足以构成一棵树的 n-1 条边。一颗有 n 个顶点的生成树有且仅有 n-1 条边，如果生成树中再添加一条边，则必定成环。
  5. 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

# 👉应用1️⃣:生成树

在图论中，常常将树定义为一个无回路的连通图
两种遍历的算法可以获得生成树：
深度优先（搜索）生成树、广度优先（搜索）生成树
在一般情况下，图中的每条边若给定了权，这时，我们所关心的不是生成树，而是生成树中边上权值之和。若生成树中每条边上权值之和达到最小，称为最小生成树。

# 👉应用2️⃣:最小生成树

# 最小生成树的两种方法

避圈法：
第一种最小生成树：普里姆算法（prim）
第二种最小生成树：克鲁斯卡尔算法（kruskal）
破圈法：运筹学最小生成树破圈法

避圈法是:你一直找最短的边然后保留下来，前提是不会形成回路
破圈法是：看见回路就找那个回路最长的边然后消除掉，然后再找下一个回路最长的边消除。算法结束:当剩下的边=结点数-1 的时候。

# 1️⃣最小生成树算法：普里姆算法（prim）

普里姆算法思想：在图中任取一个顶点 K 作为开始点，令 U={k}，W=V-U，其中 V 为所有顶点集，然后找一个顶点在 U 中，另一个顶点在 W 中的边中最短的一条，找到后，将该边作为最小生成树的树边保存起来，并将该边顶点全部加入 U 集合中，并从 W 中删去这些顶点，然后重新调整 U 中顶点到 W 中顶点的距离，使之保持最小，再重复此过程直到 W 为空集为止。

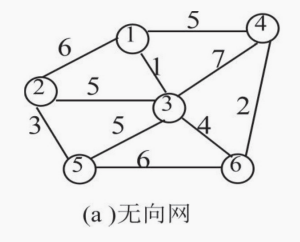
undirected-graph

算法思想过程：
设置2个数据结构：

lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0，说明以i为终点的边的最小权值=0,也就是表示i点加入了MST

visitInfo: 表示已经访问的节点

  1. 我们假设1是起始点，进行初始化（∞代表无限大，即无通路）： // 数组下标加1是节点数字
    1 => 3 lowcost[1]=6 lowcost[2]=1 lowcost[3]=5 lowcost[4]=Infinity lowcost[5]=Infinity
    3 => 6 lowcost[1]=5 lowcost[3]=5 lowcost[4]=6 lowcost[5]=4
    6 => 4 lowcost[1]=5 lowcost[3]=2 lowcost[4]=6
    4 => 2 lowcost[1]=5 lowcost[4]=6 2 => 5 lowcost[4]=3

上面的图用表格表示如下：
其中（∞代表没有关系）

1 2 3 4 5 6
1 ∞ 6 1 5 ∞ ∞
2 6 ∞ 5 ∞ 3 ∞
3 1 5 ∞ 7 5 4
4 5 ∞ 7 ∞ ∞ 2
5 ∞ 3 5 ∞ ∞ 6
6 ∞ ∞ 4 2 6 ∞

例: V={1，2，3，4，5，6} 则 U={} W={1,2,3,4,5,6}
实现prim算法过程:

u w
{1} {2,3,4,5,6}
{1,3} {2,4,5,6}
{1,3,6} {2,4,5}
{1,3,6,4} {2,5}
{1,3,6,4,2} {5}
{1,3,6,4,2,5} {}
# 2️⃣最小生成树算法:克鲁斯卡尔算法（kruskal）

克鲁期卡尔算法的基本思想是：将图中所有边按权值递增顺序排列，依次选定取权值最小的边，但要求后面选 取的边不能与前面选取的边构成回路，若构成回路，则放弃该条边，再去选后面权值较大的边，n 个顶点的图中，选够 n-1 条边即可。

时间复杂度：
克鲁斯卡尔算法的时间复杂度主要由排序方法决定，而克鲁斯卡尔算法的排序方法只与网中边的条数有关，而与网中顶点的个数无关，当使用时间复杂度为O（elog2e）的排序方法时，克鲁斯卡尔算法的时间复杂度即为O（log2e），因此当网的顶点个数较多、而边的条数较少时，使用克鲁斯卡尔算法构造最小生成树效果较好 。

算法步骤：
a、对图的存储结构，按照权值，从小到大排序。 b、对并查集进行初始化，即把每一个位置中的值初始化为其对应下标。(上图是已经初始化好的) c、选取存储结构的第一项(最小项)，查询该边所对应的顶点在并查集中是否同源，同源则进行e，不同源则进行d d、若不同源，则把该边加入生成树，并计算和；修改前者的根在并查集中位置的值为后者的根。如下图：第一项(0,1)不同源，顶点0的根为0，顶点1的根为1，设a为并查集数组，把a[0] = 1，即把并查集中下标为0的位置中的值修改为1。这样，(0,1)这条路径就加入了最小生成树。

【注】：并查集-图的连通性 (opens new window)

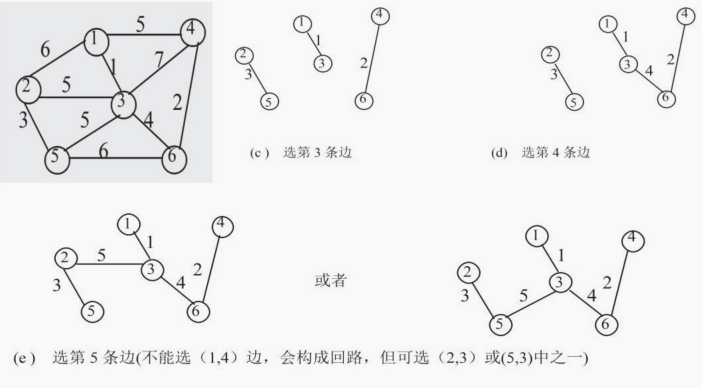
undirected-graph 克鲁斯卡尔最小生成树过程 kruskal

避圈法：
我们熟知的 Prim 算法和 Kruskal 算法可以用来找到最小生成树，不过这两种算法的思想其实是一致的：一开始我只有有限的信息，无论是所有顶点做加边法，还是所有的边做加点法，一开始的信息都是不完整的。其实无论是加点还是加边，本质上是从最小的权的边开始，添加的是在未选中的边中的最小权值边，原理都是使用了 MST 性质去做的。 在做 Prim 算法和 Kruskal 算法时我们比较关心每添加了一次边就检查看看有没有出线回路，因为生成树是不能有回路。那也就是说我要避免回路的出现，在重复添加最小权值边时就能保证将最小生成树添加出来，这种手法就被称为避圈法。 破圈法：
现在我有全套的信息，我要怎么把最小生成树找出来？由于最小生成树是 n 个顶点 n - 1 条边，因此我需要将边的数量减少到 n - 1 条，一旦我满足了这点就可以认为是找到了最小生成树。

算法思想：

  1. 找到权值最大的边，判断这条边是否存在回路，存在则删除，如果对存在回路没有影响，则保留
  2. 从权值大到权值小依次判断，边的数据缩短到n-1，则构造完成

# 👉应用3️⃣:最短路径

讨论最短路径的方法有两种：单源点最短路径、所有顶点对的最短路径。

# 单源点最短路径：迪杰斯特拉（Dijkstra）算法

定义：单源点最短路径是指：给定一个出发点（单源点）和一个有向网 G=（V，E），求出源点到其它各顶点之间的最短路径。
问题：怎样求出单源点的最短路径呢？
解答：将源点到终点的所有路径都列出来，然后在里面选最短的一条即可。但是这样做用手工方式可以，当路径特别多，显的特别麻烦，并且没有什么规律，不能用计算机算法实现。
方法： 迪杰斯特拉（Dijkstra）在做了大量观察后，首先提出了按路长度递增序产生各顶点的最短路径算法，我们称之为迪杰斯特拉算法
算法思想：设 V 为网中所有顶点集合，设置并逐步扩充一个集合 S，存放已求出其最短路径的顶点，则尚未确定最短路径的顶点集合 V-S：按路径长度递增的顺序逐个把 V-S 中的顶点加到 S 中，直到 S 中包含全部顶点，而 V-S 为空。通俗的讲就是每次在全部中选最小值放进去，再对比再找最小值。

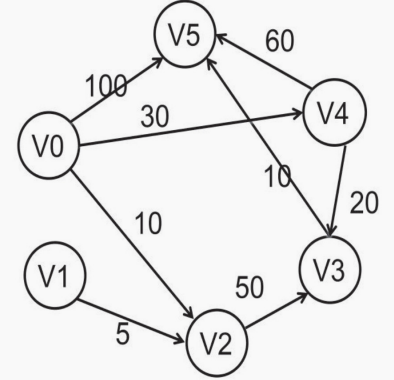
dijkstra
终点 从V0到各终点的最短路径
i=1 i=2 i=3 i=4 i=5
V1∞∞∞∞∞
V210(V0,V2)
V3∞60(V0,V2,V3)50(V0,V4,V3)
V430(V0,V4)30(V0,V4)
V5100(V0,V5)100(V0,V5)90(V0,V4,V5)60(V0,V4,V3,V5)
VKV2V4V3V5无
PathV0-V2V0-V4V0-V4-V3V0-V4-V3-V5
S{V0,V2}{V0,V2,V4}{V0,V2,V4,V3}{V0,V2,V4,V3,V5}

这个算法的过程有比prim算法的过程稍微多一点点步骤，但是思想确实巧妙的，也是贪心原理，它的目的是求某个源点到目的点的最短距离，总的来说，dijkstra算法也就是求某个源点到目的点的最短路，求解的过程也就是求源点到整个图的最短距离，次短距离，第三短距离等等（这些距离都是源点到某个点的最短距离）。求的是原点到所有点的最短距离，最后给出目的点就能直接通过查表获得最短距离。

# 所有顶点对之间的最短路径：Floyd 算法

所有顶点对之间的最短路径是指：对于给定的有向网 G=（V，E），要对 G 中任意对顶点有序对 V、W（V<>W）,找出 V 到 W 的最短距离和 W 到 V 的最短距离。
解决此问题有效的方法：轮流以每一个顶点为源点，重复执行迪杰斯特拉算法 n 次，可求得每一对顶点之间的最短路径，总的时间复杂度为 O（n^3）,效率太低，于是出现了 Floyd 算法。

Floyd 算法思想：
将 V1 到 Vj 的最短路径长度初始化，即 D[i][j]为项点 i 到 j 的路径长度，然后进行 n 次比较和更新。通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。

Floyd-warshall算法描述：

// floydWarshell
let n = 4;
let arcs = [
    [0, 3, Infinity, 7],
    [8, 0, 2, Infinity],
    [5, Infinity, 0, 1],
    [2, Infinity, Infinity, 0]
]

function floydWarshell() {
    for (let k = 0; k < n; k++) {
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < n; j++) {
                arcs[i][j] = min(arcs[i][j], arcs[i][k] + arcs[k][j])
            }
        }
    }
}

function min(num1, num2) {
    return num1 < num2 ? num1 : num2;
}

floydWarshell();
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
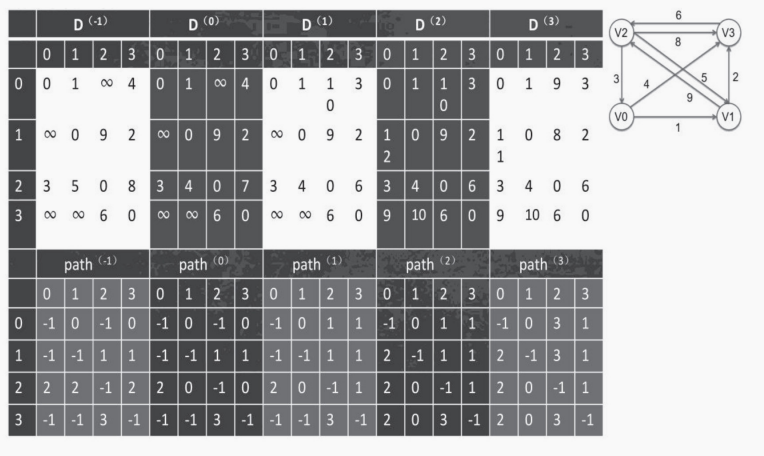
floyd

floyd 在滑块法中就是等于 0 的时候 那一行一列不动。看其它的最小的是哪个然后更新。上面的矩阵更新了，下面的矩阵也要跟着更新。从 0 到 3 依次更新，每次更新时候加入一个顶点。然后看看整个矩阵有没有新的最短路径生成。有的话就更新没有的话就不更新。

# 👉应用4️⃣:拓扑排序

通常我们把计划、施工过程、生产流程等都当成一个工程，一个大工程常常被划分成许多较小的子工程，这些子工程称为活动，这些活动完成时，整个工程也就完成了。

# AOV 网介绍

在这种有向图中，顶点表示活动，有向边表示活动的优先关系，这有向图叫做顶点表示活动的网络（Actrie On Vertices）简称 AOV 网。
在 AOV 网中，<i,j>有向边表示 i 活动应先于 j 活动开始，即 i 活动必须完成后，j 活动才可以列始，并称 i 为 j 的直接前驱，j 为 i 的直接后继。这种前驱与后继的关系有传递性，此外，任何活动 i 不能以它自己作为自己的前驱或者后继，这叫做反自反性。从前驱和后继的传递性和反自反性来看，AOV 网中不能出现有向回路（或称有向环），对工程而言，将无法进行：对程序流程而言，将出现死循环。

拓扑排序的步骤：

  1. 在 AOV 网中选一个入度为 0 的顶点且输出
  2. 在 AOV 网中删除此顶点及该顶点发出来的所有有向边
  3. 重复 1，2 两步，直到 AOV 网中所有顶点都被输出或网中不存在入度为 0 的顶点。

# 👉应用5️⃣:关键路径

若以带权有向图的顶点代表事件（event）或工程进展状态，用弧表示活动，弧上的权值表示完成该活动所需要的时间，则这样的带权有向图称为 AOE 网（Activity On Edge Network）
（1）只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始。
（2）只有在进入某点的各有向边所代表的活动都已结束，该顶点所代表的时事件才能发生。
关键路径（临界路径）：在 AOE 网络中从源点到汇点（结束顶点）的最长路径。关键路径上的活动为关键活动。

# 总结

1：Prim是计算最小生成树的算法，比如为N个村庄修路，怎么修花销最少。

Dijkstra是计算最短路径的算法，比如从a村庄走到其他任意村庄的距离。

2：Prim算法的更新操作更新的·距离·是已访问集合到未访问集合中各点的距离；

Dijkstra算法的更新操作更新的·距离·是源点到未访问集合中各点的距离；

  1. Prim在稠密图中比Kruskal优，在稀疏图中比Kruskal劣。

图的存储和遍历 (opens new window) 最短路径问题 (opens new window) floyd-warshell (opens new window)

上次更新: 2025/04/07, 01:42:58
排序算法总结
串的模式匹配

← 串的模式匹配→

Copyright © 2015-2025 Glitz Ma